Understanding The Unit Circle With Tangent Values: A Comprehensive Guide
Table of Contents
- Introduction
- What is a Unit Circle?
- Understanding Tangent Values
- How to Find Tangent Values on the Unit Circle
- Applications of the Unit Circle in Mathematics
- Common Mistakes When Using the Unit Circle
- Tips for Mastering the Unit Circle
- Real-Life Examples of Unit Circle Applications
- Tools and Resources for Learning the Unit Circle
- Conclusion
Introduction
The unit circle with tangent values is a fundamental concept in trigonometry that every student must understand to excel in mathematics. This concept is not only essential for solving mathematical problems but also plays a crucial role in various fields such as physics, engineering, and computer science. The unit circle is a circle with a radius of 1, centered at the origin of a coordinate plane. It helps in visualizing trigonometric functions like sine, cosine, and tangent, making it easier to comprehend their behavior.
In this article, we will explore the unit circle with tangent values in detail. We will break down the concept into manageable sections, providing clear explanations and examples to ensure you grasp the topic thoroughly. Whether you are a beginner or looking to deepen your understanding, this guide will serve as a valuable resource.
By the end of this article, you will not only understand the unit circle with tangent values but also appreciate its significance in both theoretical and practical applications. Let’s dive into the world of trigonometry and uncover the mysteries of the unit circle.
Read also:Understanding The Zodiac Year 1965 Insights And Meanings
What is a Unit Circle?
A unit circle is a circle with a radius of 1 unit, centered at the origin (0, 0) of a Cartesian coordinate system. It is a foundational tool in trigonometry, used to define and visualize trigonometric functions such as sine, cosine, and tangent. The unit circle provides a geometric representation of these functions, making it easier to understand their relationships and properties.
One of the key features of the unit circle is that it simplifies the calculation of trigonometric values. For any angle θ, the coordinates of the point where the terminal side of the angle intersects the unit circle are (cos θ, sin θ). This relationship is crucial for understanding how trigonometric functions behave as the angle changes.
The unit circle is also helpful in understanding periodicity. Since the circle is continuous, trigonometric functions repeat their values after every full rotation (360° or 2π radians). This periodic nature is essential in various applications, including wave motion and oscillations.
Understanding Tangent Values
The tangent function, often abbreviated as tan, is one of the primary trigonometric functions derived from the unit circle. It is defined as the ratio of the sine and cosine of an angle: tan θ = sin θ / cos θ. On the unit circle, the tangent value corresponds to the slope of the line that connects the origin to the point on the circle defined by the angle θ.
One important aspect of the tangent function is that it is undefined at certain points. Specifically, tan θ is undefined when cos θ = 0, which occurs at angles like 90° and 270°. These points correspond to vertical asymptotes on the graph of the tangent function, highlighting its discontinuous nature.
Understanding tangent values on the unit circle is essential for solving trigonometric equations and analyzing periodic phenomena. By visualizing the unit circle, students can better grasp how tangent values change as the angle increases and identify patterns that simplify calculations.
Read also:Lindsey Sporrer In Blue Mountain State An Indepth Look At Her Role And Impact
How to Find Tangent Values on the Unit Circle
Finding tangent values on the unit circle involves a step-by-step process that combines geometric visualization and algebraic computation. Here’s how you can determine the tangent value for any given angle:
- Step 1: Locate the angle θ on the unit circle.
- Step 2: Identify the coordinates (cos θ, sin θ) of the corresponding point on the circle.
- Step 3: Use the formula tan θ = sin θ / cos θ to calculate the tangent value.
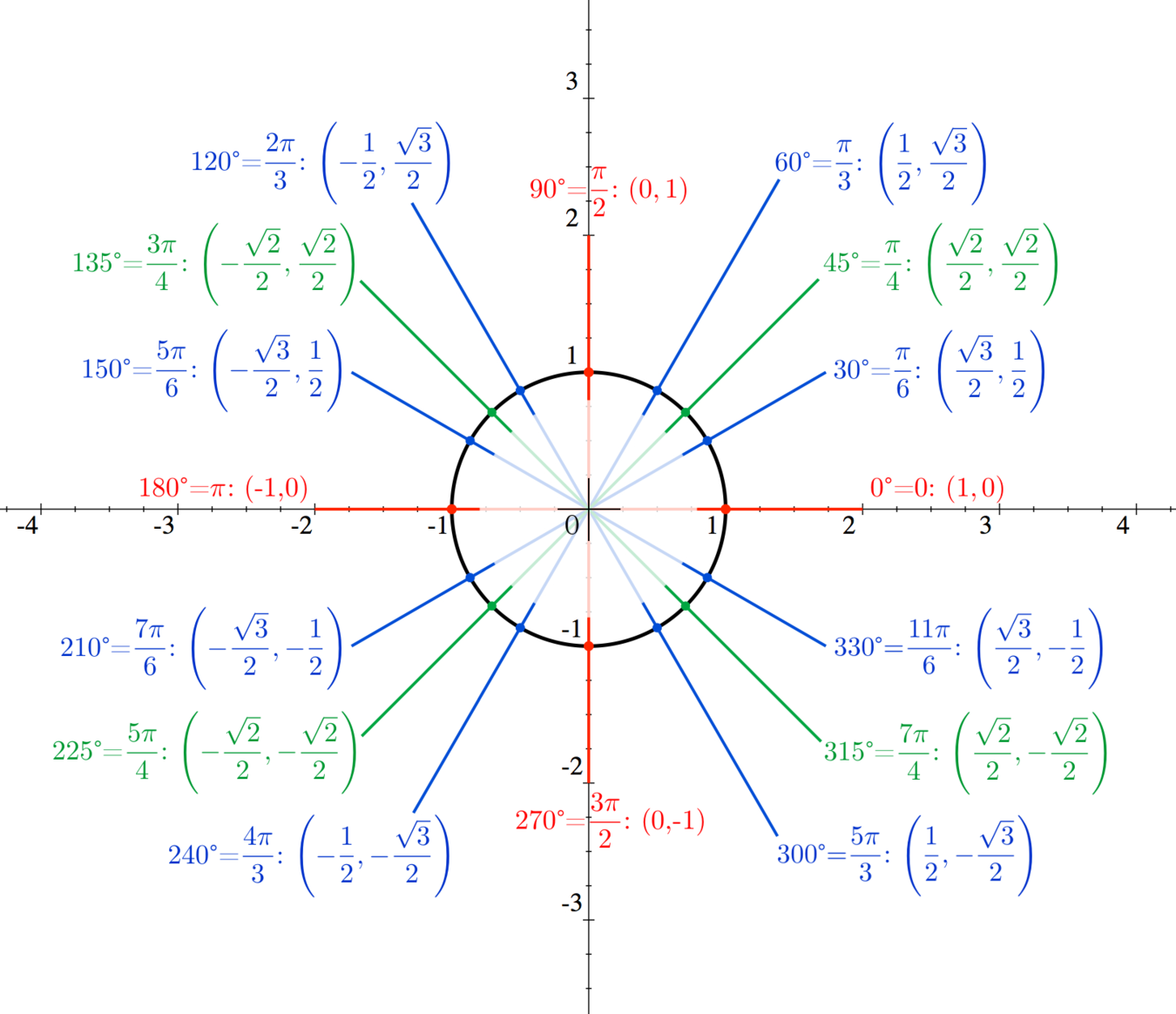
For example, at 45° (π/4 radians), the coordinates are (√2/2, √2/2). Using the formula, tan 45° = (√2/2) / (√2/2) = 1. This method works for any angle, provided that cos θ ≠ 0.
Special Angles and Their Tangent Values
Some angles have well-known tangent values that are worth memorizing. These include:
- 0°: tan 0° = 0
- 45°: tan 45° = 1
- 60°: tan 60° = √3
- 90°: tan 90° is undefined
Applications of the Unit Circle in Mathematics
The unit circle with tangent values has numerous applications in mathematics and related fields. One of its primary uses is in solving trigonometric equations. By visualizing the unit circle, students can identify solutions to equations involving sine, cosine, and tangent functions.
Another significant application is in modeling periodic phenomena. For example, the unit circle is used to describe wave motion, such as sound waves and light waves. The periodic nature of trigonometric functions mirrors the behavior of these waves, making the unit circle an invaluable tool in physics and engineering.
In computer graphics, the unit circle is used to calculate rotations and transformations. By understanding tangent values, developers can create realistic animations and simulations that mimic real-world movements.
Common Mistakes When Using the Unit Circle
While the unit circle is a powerful tool, students often make mistakes when using it. One common error is confusing the coordinates of points on the circle. Remember, the x-coordinate corresponds to cos θ, and the y-coordinate corresponds to sin θ.
Another frequent mistake is forgetting that the tangent function is undefined at certain angles. This oversight can lead to incorrect calculations or misinterpretations of graphs. Always double-check whether cos θ equals zero before calculating tan θ.
Finally, students sometimes overlook the periodicity of trigonometric functions. The unit circle repeats its values every 360°, so it’s essential to consider multiple rotations when solving problems involving angles greater than 360°.
Tips for Mastering the Unit Circle
Mastering the unit circle with tangent values requires practice and a strategic approach. Here are some tips to help you succeed:
- Memorize Key Values: Focus on memorizing the sine, cosine, and tangent values for common angles like 0°, 30°, 45°, 60°, and 90°.
- Visualize the Circle: Use diagrams and interactive tools to visualize how angles and coordinates relate to each other.
- Practice Regularly: Solve a variety of problems involving the unit circle to reinforce your understanding.
Real-Life Examples of Unit Circle Applications
The unit circle is not just a theoretical concept; it has practical applications in everyday life. For instance, in architecture, the unit circle is used to design structures with curved surfaces, ensuring stability and aesthetic appeal.
In navigation, the unit circle helps pilots and sailors determine their position and direction. By using trigonometric functions, they can calculate distances and angles with precision.
Even in entertainment, the unit circle plays a role. Animators use it to create smooth and realistic movements in video games and movies, enhancing the viewer’s experience.
Tools and Resources for Learning the Unit Circle
There are numerous tools and resources available to help you learn the unit circle with tangent values. Online calculators and graphing tools can visualize the circle and its functions, making it easier to understand their behavior.
Educational websites and textbooks often provide detailed explanations and practice problems. Additionally, interactive apps and videos can offer engaging ways to explore the unit circle.
For those seeking expert guidance, consider enrolling in online courses or hiring a tutor. These resources can provide personalized support and ensure you master the unit circle effectively.
Conclusion
In conclusion, the unit circle with tangent values is a cornerstone of trigonometry with far-reaching applications. By understanding its principles and practicing its use, you can enhance your mathematical skills and apply them to real-world problems.
We encourage you to explore the resources mentioned in this article and continue your learning journey. If you found this guide helpful, please share it with others who might benefit. For more insights into mathematics and related topics, check out our other articles. Happy learning!
Barry Manilow's "Mandy": Exploring The Meaning Behind The Iconic Song
Unlocking The Mysteries Of Angel Numbers 1313: Meaning, Significance, And Guidance
Best Email Marketing Service For Small Business: A Comprehensive Guide
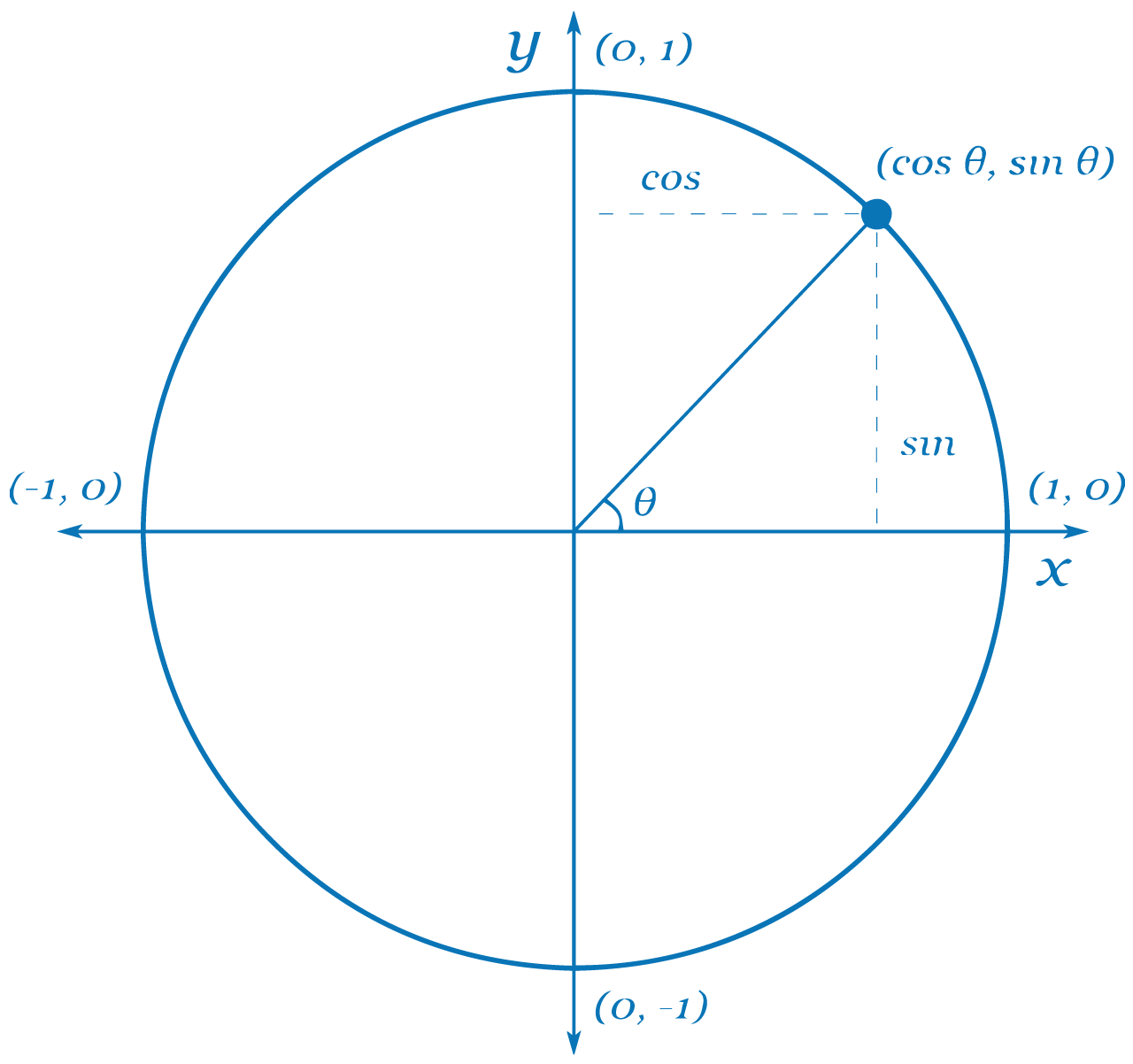
Table Of Tangent Values For Unit Circle Review Home Decor
Unit Circle Essential Trigonometric Values Math Wiki